07自动求导

7.1自动求导

• 向量链式法则

  • 标量链式法则

    

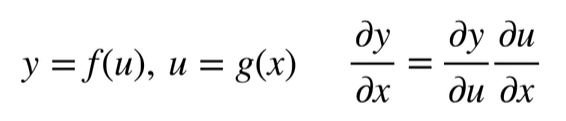
  • 拓展到向量

    

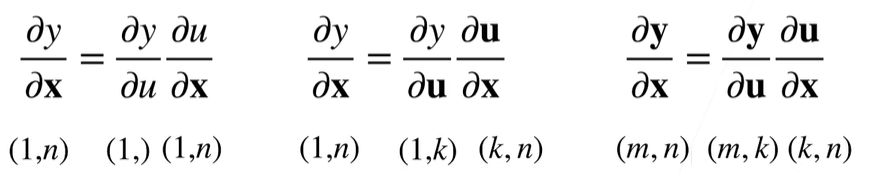
【举例】

假设

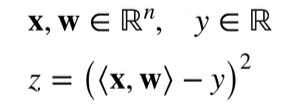
计算

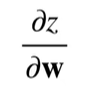
先分解

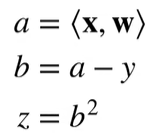
得到：

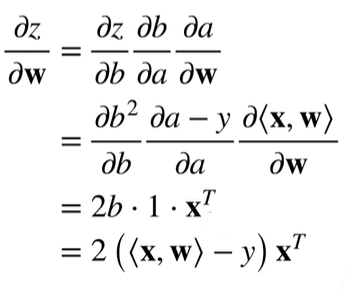
【举例】

假设

计算：

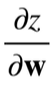
分解：

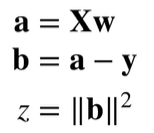
得到：

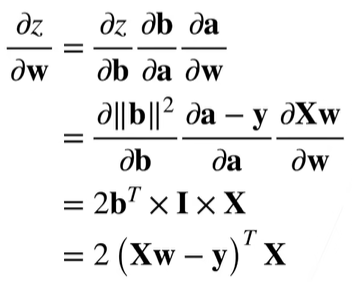
• 自动求导

  • 自动求导计算一个函数在指定值上的导数

  • 它有别于

    • 符号求导

      

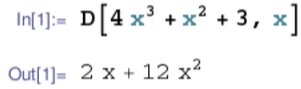
    • 数值求导

      

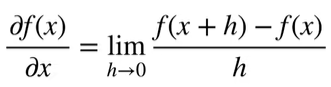
• 计算图

  • 将代码分解成操作子
  • 将计算表示成一个无环图
  • 显示构造（Tensorflow/Theano/MXNet）
  • 隐式构造（PyTorch/MXNet）

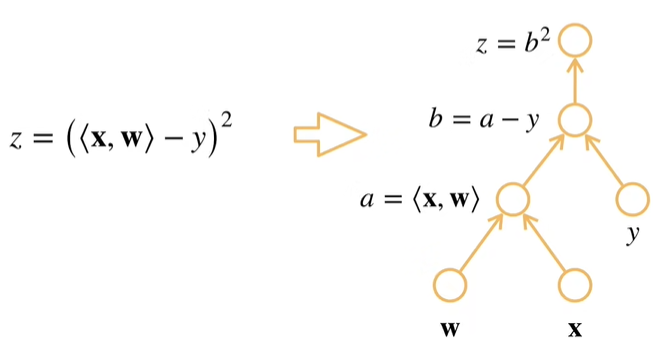
相当于告诉机器我是如何一步一步地计算地：

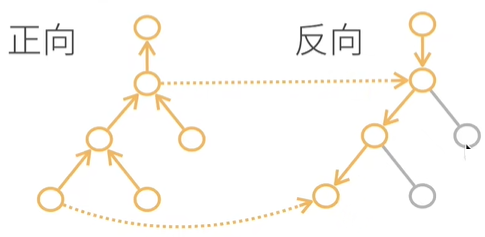
• 自动求导地两种模式

  • 链式法则

    

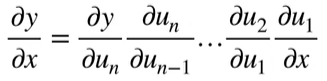
  • 正向积累

    

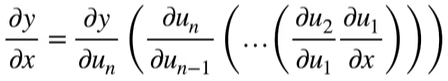
  • 反向积累、又称反向传递 （backforward）

    

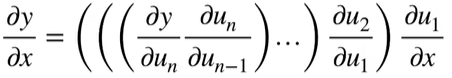
• 反向积累

  

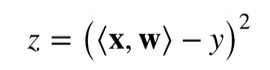
先看正向，正向就是自计算图的底端，从下往上开始计算

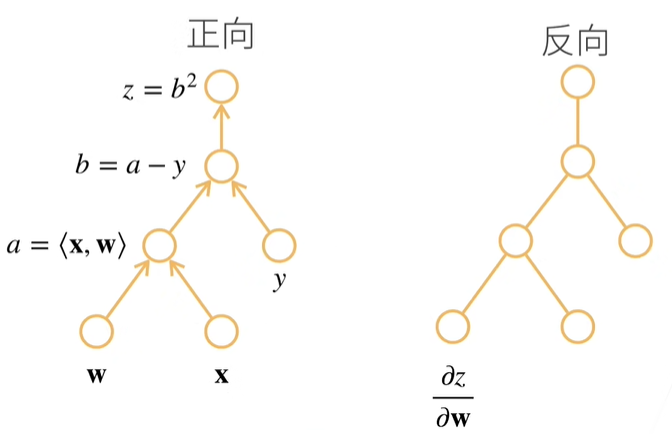
当正向算完以后，就可以反向积累了。

首先，先求 $z$ 关于 $b$ 的导数，算完的结果是 $2b$ ，显然这里的 $b$ 反向积累时，不知道它的值究竟是多少，怎么办呢？我们可以使用之前正向计算过程中留下的结果，也就是读取之前运行的结果

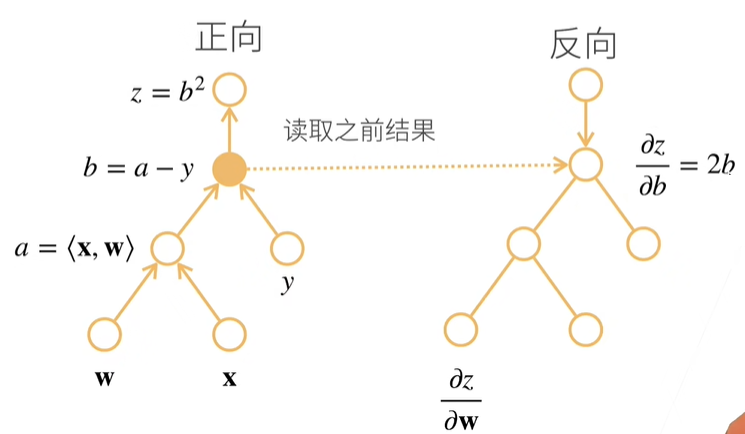
同理，我们可以计算 $z$ 关于 $a$ 的导数，这里的 $b$ 就可以使用上面的 $2b$ 中的 $b$ 了。

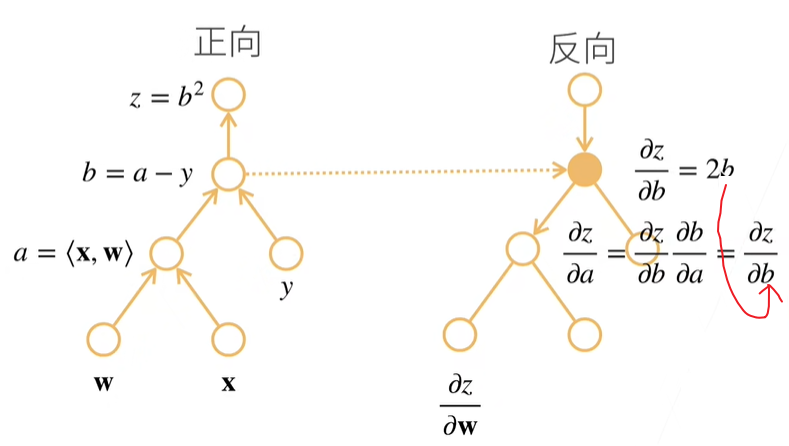
最后，我们计算 $z$ 关于 $w$ 的导数，其中的 $a$ 可以取自正向计算时得到的结果

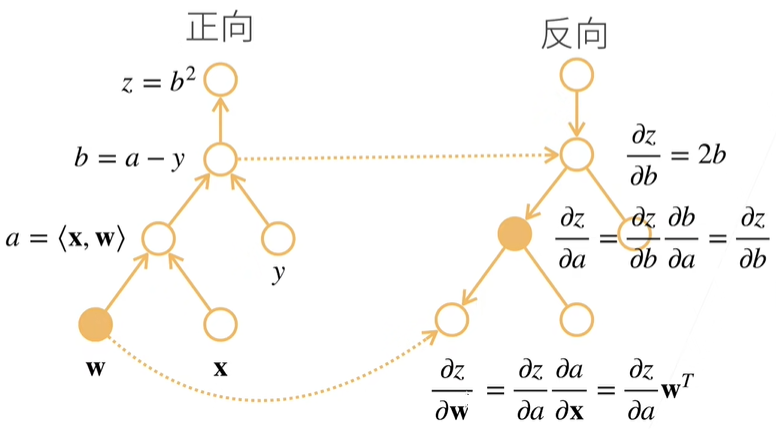
• 反向累积小结

  • 前向：执行图，存储中间结果

  • 反向：从相反方向执行图

    • 去除不需要的枝

      

• 复杂度

  • 计算复杂度：O(n), n是操作子个数
    • 通常正向和反向的代价类似
  • 内存复杂度：O(n)，因为需要存储正向的所有中间结果
  • 跟正向累积对比：
    • O(n)计算复杂度用来计算一个变量的梯度
    • O(1)内存复杂度

7.2自动求导实现

假设我们想对函数 $y = 2 \boldsymbol {x}^T\boldsymbol {x}$ 关于列向量 $\boldsymbol {x}$ 求导

在我们计算 $y$ 关于 $\boldsymbol {x}$ 的梯度之前，我们需要一个地方来存储梯度。

现在我们计算 $y$ 。

通过调用反向传播函数来自动计算 $y$ 关于 $\boldsymbol {x}$ 每个分量的梯度。

现在让我们计算 $\boldsymbol {x}$ 的另一个函数。

深度学习中，我们的目的不是计算微分矩阵，而是批量中每个样本单独计算的偏导数之和。

将某些计算移动到记录的计算图之外，用于固定网络中的某些参数

即使构建函数的计算图需要通过 Python 控制流（例如，条件、循环或任意函数调用）我们任然可以计算得到变量的梯度。

工作原理是：隐式计算流：首先看我们的函数，你会发现，整个函数的返回值总是取决于 b 的值或者是你输入的 a 的值。每一次计算的时候，PyTorch会在背后将计算图存储下来，然后倒着做一遍就可以正确答案了。同时计算更慢。

7.3QA