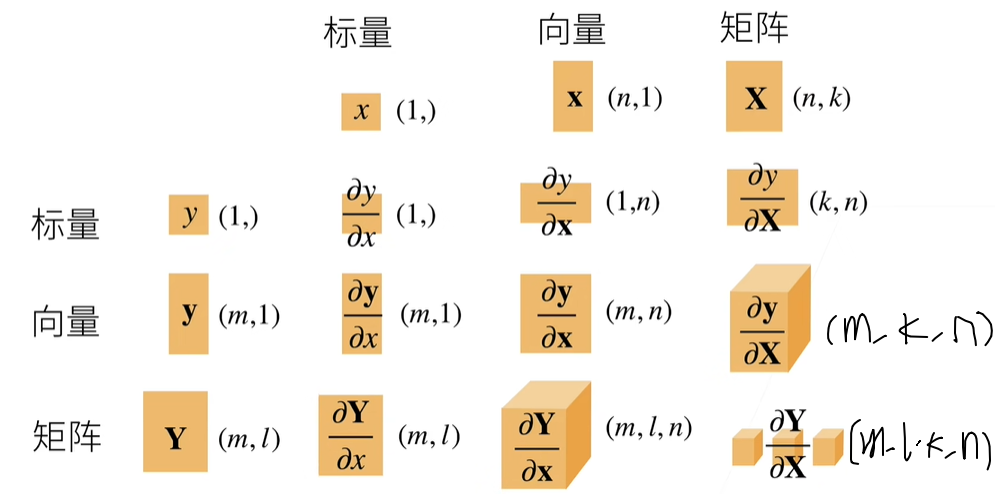
06矩阵计算

6.1矩阵计算

• 标量导数

• 导数是切线的斜率

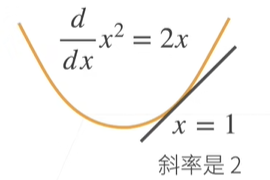
• 亚导数
  • 将导数拓展到不可微的函数

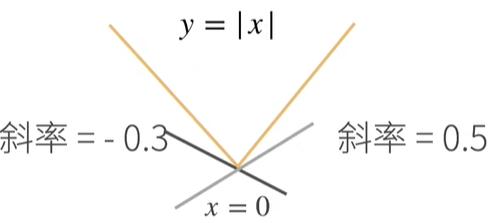
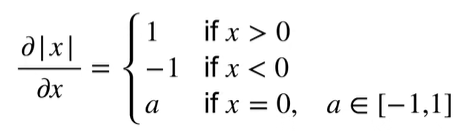
另一个例子

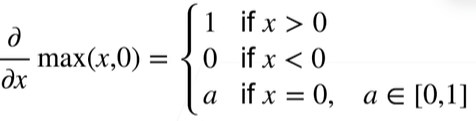
• 梯度
  • 将导数拓展到向量

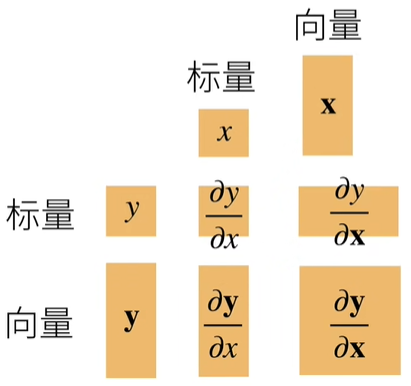
• $\frac{\partial y}{\partial x}$
  • 列向量的导数是行向量

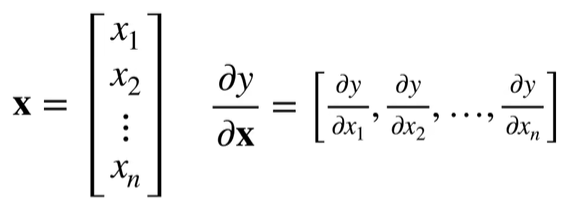
【举例】

$$\frac{\partial x_1^2}{\partial x} + 2x_2^2=[2x_1 + 4x_2]$$

方向 $(2, 4)$ 与等高线正交

如何理解：前面的函数可以画作是等高线，可以看作是一座山，现取任意一点 $(x_1, x_2) = (1, 1)$ ，经过这个点做等高线的切线（可以看作是上面函数的导数），而这个切线的垂线方向恰好可以使用我们所谓的梯度函数 $[2x_1, 4x_2]$ 计算出来。

梯度和等高线是正交的，指向的是等高线变化最大的方向。也就是机器学习求解的核心思想。

【举例】

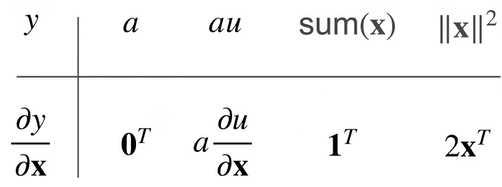
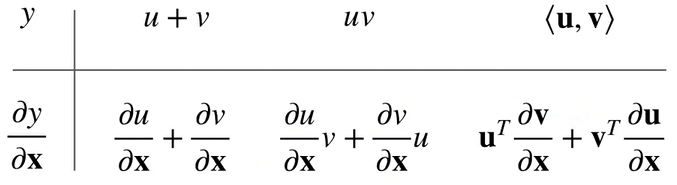
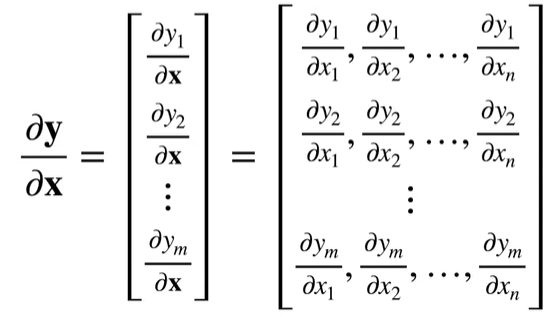
• $\frac{\partial y}{\partial x}$

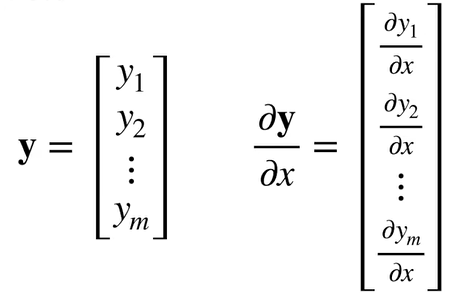
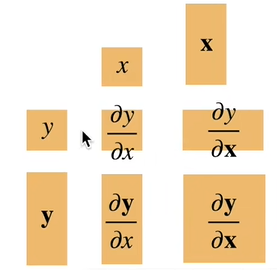
$\frac{\partial y}{\partial x}$是行向量，$\frac{\partial y}{\partial x}$是列向量，这个被称为分子局部符号，反过来的版本就叫分母布局符号

• $\frac{\partial y}{\partial x}$

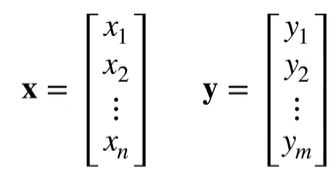
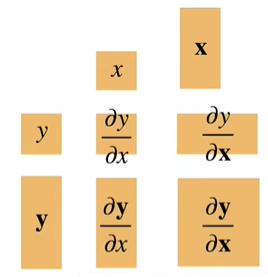
【举例】

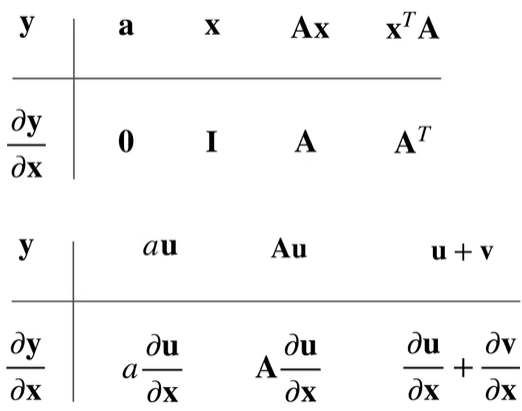
• 拓展到矩阵

6.2QA