05线性代数

5.1线性代数
标量
简单操作
长度
向量
简单操作
长度
【举例】
$c = a + b$
$c = a * b$

- 点乘
- 正交

矩阵
- 简单操作
- 乘法(矩阵乘以向量)
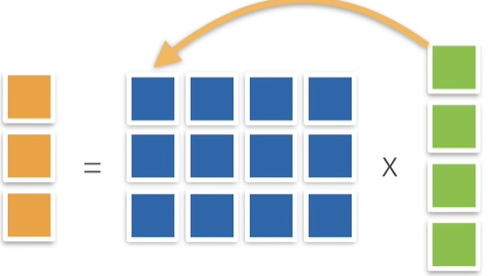
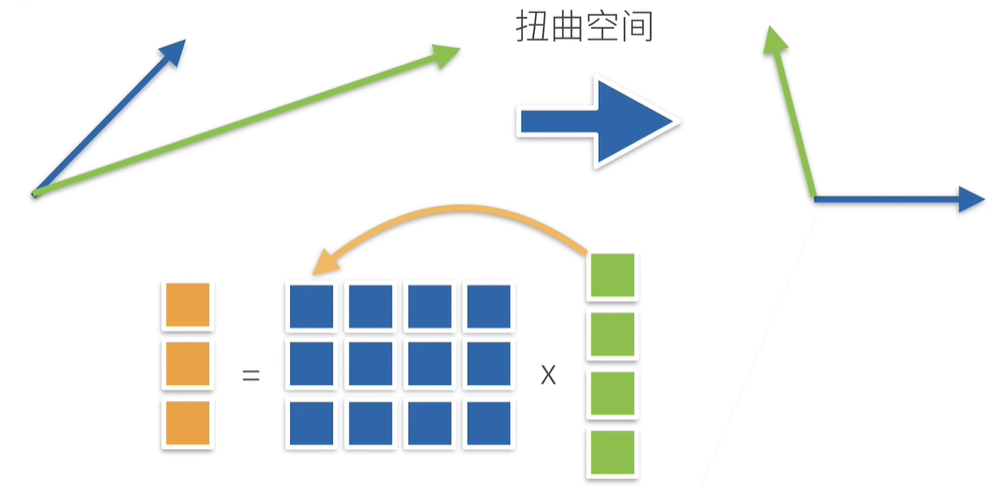
直观上理解矩阵乘法:向量可以看作空间,矩阵可以看作是特定的工具,向量与特定的矩阵相乘后,将会使得向量变得扭曲,也就是变换到另一个空间中
- 范数
- 取决于如何衡量 b 和 c的长度
- 常见的范数
- 矩阵范数:最小的满足的上面公式的值
- Frobenius 范数
特殊矩阵
- 对称和反对称
- 正定

- 正交矩阵
- 所有行都相互正交
- 所有行都有单位长度 $u$
- 可以写成
- 置换矩阵
- 置换矩阵是正交矩阵
- 特征向量和特征值
- 不被矩阵改变方向的向量$x$(但长度可能会改变)
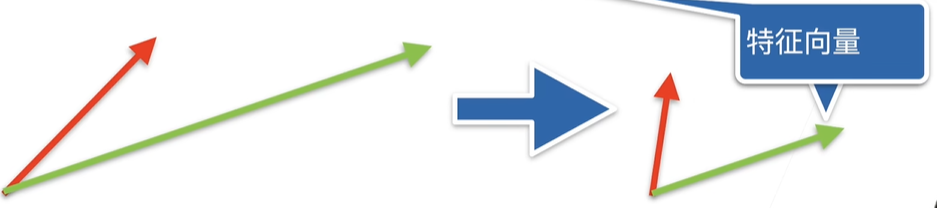
- 对称矩阵总是可以找到特征向量
5.2线性代数实现
标量由只有一个元素的张量表示

你可以将向量视为标量值组成的列表

通过张量的索引来访问任一元素

访问张量的长度

只有一个轴的张量,形状只有一个元素

通过指定两个分量 $m$ 和 $n$ 来创建一个形状 $m * n$ 的矩阵
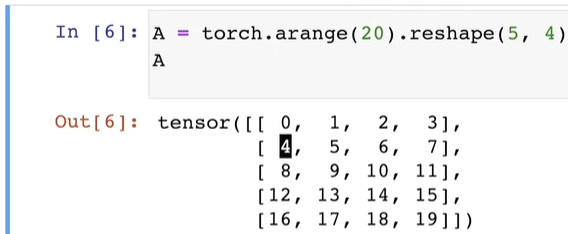
矩阵的转置

对称矩阵(symmetric matrix)$A$ 等于其转置:$A = A^T$


就像向量是标量的推广,矩阵是向量的推广一样,我们可以构建具有更多轴的数据结构 代表2个具有3 * 4结构的矩阵的组合

给定具有相同形状的任何两个张量,任何按元素二元运算的结果都将是相同形状的张量


两个矩阵的按元素的成绩称为 哈达玛积(Hadamard product)(数学符号)⊙


计算其元素的和

表示任意形状张量的元素和

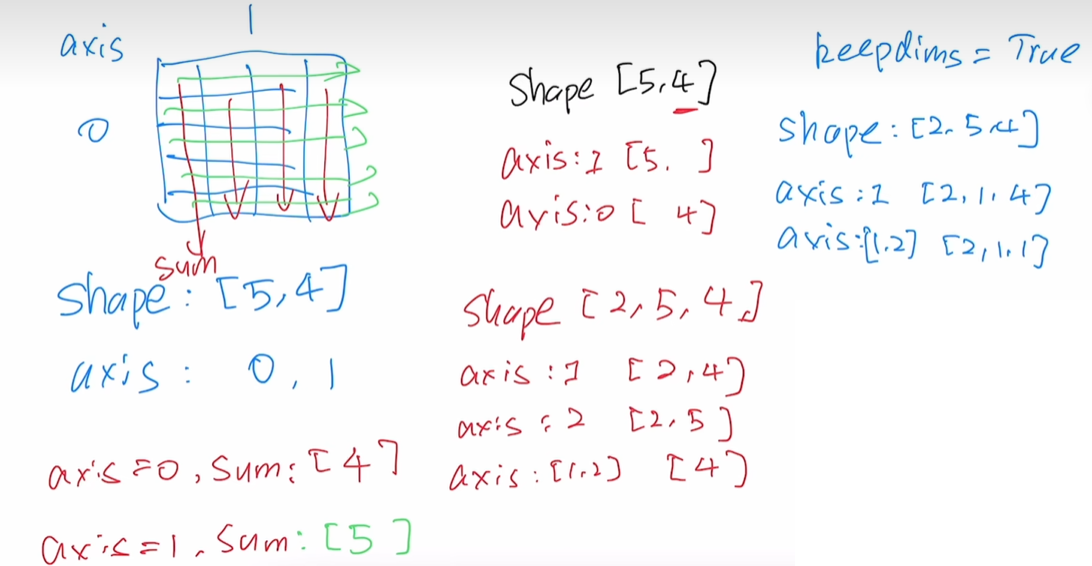
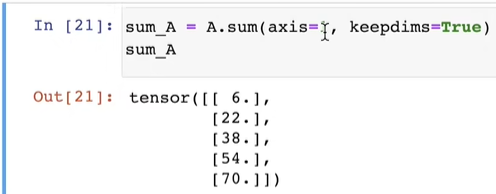
指定求和汇总张量的轴
axis=0 意味着对 2 这一维度进行求和,剩下的两个维度留下来了。


axis=1 意味着对 5 这一维度进行求和,剩下的两个维度留下来了。

也可以指定其中的多个维度进行求和,其余的维度留下来


下面解释一下是怎么按特定轴求和的
1 | 原始的tensor.size([2, 5, 4]), 一共是40个数 |
一个与求和相关的量是 平均值(mean 或 average)

计算总和或均值时保持轴数不变
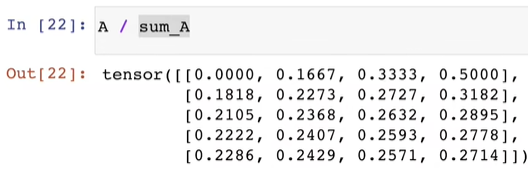
通过广播将 $A$ 除以 sum_A
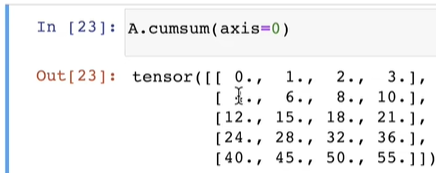
某个轴计算 $A$ 元素的累积总和
点积是相同位置的按元素乘积的和4

我们可以通过执行按元素乘法,然后进行求和来表示两个向量的点积

矩阵向量积 $Ax$ 是一个长度为 $m$ 的列向量,其 $i^{th}$ 元素是点积 $a_i^Tx$

我们可以将矩阵-矩阵乘法 $AB$ 看作是简单地执行 $m$ 次矩阵-向量积,并将结果拼接在一起,形成一个 $n * m$ 的矩阵

$L_2$ 范数是向量元素平方和的平方根

$L_1$ 范数,它表示为向量元素的绝对值之和:

矩阵的 弗罗贝尼乌斯范数 (Frobenius norm) 是矩阵元素的平方和的平方根:

5.3按特定轴求和