GBDT

​ GBDT为梯度提升决策树（Gradient Boosting Decision Tree），是一种以回归决策树为 弱学习器的集成学习模型。GBDT集成学习模型通常使用CART决 策树（回归树）模型作为弱学习器。

​ 提升树算法(Boosting Decision Tree)：

• 提升树是迭代多棵回归树来共同决策。当采用平方 误差损失函数时，每一棵回归树学习的是之前所有 树的结论和残差，拟合得到一个当前的残差回归树。
• 残差 = 真实值- 预测值。
• 提升树即是整个迭代过程生成的回归树的累加。

例：训练一个提升树模型来预测年龄 训练集只有4个人，A,B,C,D，他们的年龄分别是 14,16,24,26。其中A、B分别是高一和高三学生；C,D 分别是应届毕业生和工作两年的员工。样本中有购物 金额、上网时长、经常到百度知道提问等特征。

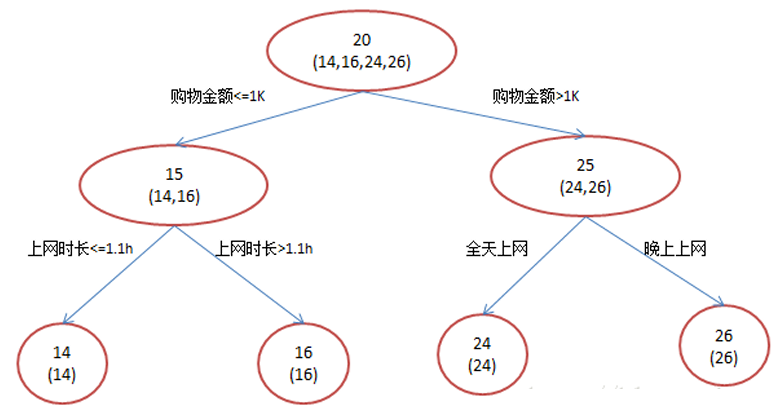
提升树过程如下：由于数据太少，限定叶子节点最多有两个，即每棵树 都只有一个分枝，并且限定只学习两棵树。第一棵树，由于A,B年龄较为 相近，C,D年龄较为相近，4人被分为两拨，每拨用平均年龄作为预测值 。拿残差替代A,B,C,D的原值，到第二棵树去学习，如果预测值和它们的残差相等，则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了。第二棵树只有两个值1和-1，直接分成两个节点。此时所有人的残 差都是0，即每个人都得到了真实的预测值。

现在A,B,C,D的预测值都和真实年龄一致

A: 14岁高一学生，购物较少，经常问学长问题； 预测年龄A = 15 – 1 = 14

B: 16岁高三学生；购物较少，经常被学弟问问题； 预测年龄B = 15 + 1 = 16

C: 24岁应届毕业生；购物较多，经常问师兄问题； 预测年龄C = 25 – 1 = 24

D: 26岁工作两年员工；购物较多，经常被师弟问问题； 预测年龄D = 25 + 1 = 26

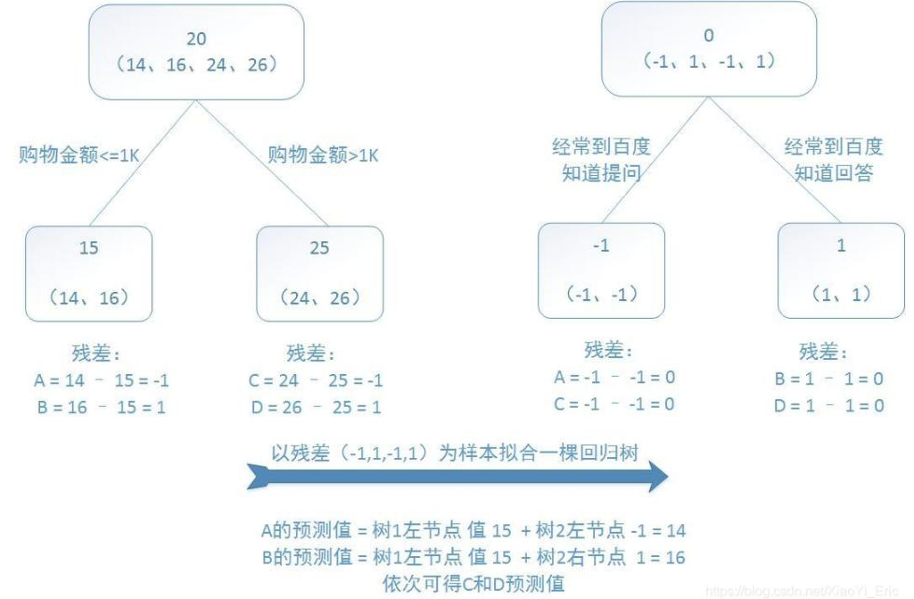
从例子很直观看到，预测值等于所有树值得累加，如A的预测值 = 树1左节点值(15)+树2左节点(-1)=14。

因此，给定当前模型fm-1(x)，只需要简单的拟合当前模型的残差。 累加每棵回归树的结论，得出最终的预测值.现将回归问题的提升 树算法叙述如下：

梯度的大小反映了当前预测值与目标值之间的距离。因 此，除第一棵决策树使用原始预测指标建树，之后的每一棵 决策树都用前一棵决策树的预测值与目标值计算出来的负梯 度来建树。相当于给分错的样本加权多次分类，使样本最终 残差趋近于0。

由于是对目标残差或增量进行建模预测，因此 GBDT模型只需把过程中每一棵决策树的输出结果累加，便 可得到最终的预测输出。

设某个回归任务的训练样本数据集为$D={(X_1, y_1), (X_2, y_2),…,(X_n, y_n)}$,根据样本集$D$构造第一 个弱学习器的初始回归决策树$L_0$，对于$D$中任意给定的一个训练样本$X$，决策树$L_0$对$X$的预测输出与其标记值$y$之间的误差为：

$$e(L_0(X))=\frac{1}{2}[L_0(X)-y]^2$$

使用上述函数作为优化的目标函数改进模型$L_0$，使用梯度下 降法实现对上述优化问题的求解，则对上式求导可求得如下梯度

$$\frac{\partial e(L_0(X))}{\partial L_0(X)}=L_0(X)-y$$

梯度的反方向为$y-L_0(X)$，应对模型$L_0(X)$往该方向进行调整。

由于模型$L_0(X)$ 的更新方向$y-L_0(x)$为训练样本标 记值与该模型预测结果之差，即模型$L_0(X)$的的预测误差 ，可构造一个新的模型$L_1(X)$进行拟合。

在对样本$X$进行预测时，由于$L_1$对于$X$的输出是对$L_0$的输出的某个校正量，且校正方向一定是误差$e$减小的 方向，故这两个模型的输出之和$L_0(X)+L_1(X)$一定比$L_0(X)$更加接近样本真实值$y$。

GBDT集成学习算法正是根据上述思路通过迭代方 式逐步构造多个弱学习器，根据训练样本数据集$D$构造 一个新的数据集$T_1$，并使用$T_1$1构造一个新的回归决策树模型$L_1(X)$作为GBDT，集成学习模型的一个新增弱学习器。$T_1$的具体形式如下：

$$T_1={(X_1, \nabla_1), (X_2, \nabla_2),...,(X_n, \nabla_n)}$$

其中$\nabla_i = y_i-L_0(X_i)$

GBDT集成学习算法的基本步骤如下：

（1）构造初始学习器$L^0(X)$。令$t=0$，根据下式构建初始回归树$L^0(X)=L_0(X)$

$$L_0(X)=arg_{c}min\sum_{X_i, y_i\in D}J(y_i,c)$$

其中$L_0(X)$为只有一个根节点的初始回归决策树，$c$为使得目标 函数最小化的模型参数，$J(y_i,c)$为损失函数。

这里采用平方误差损失函数，即有：

$$J(y,g(x))=\frac{1}{2}(y-g(x))^2$$

其中$y$为为样本真实值或标注值，$g(x)$为单个回归决策树模型的预测。

（2）令$t=t+1$，并计算数据集$D$中每个训练样本的负梯度$\nabla_i$：

$$\nabla_i=-[\frac{\partial J(y,L(X_i)}{\partial L(X_i)}]_{L(X)=L^t(X)}$$

（3）构建新的训练样本集$T_t$：

$$T_1={(X_1, \nabla_1), (X_2, \nabla_2),...,(X_n, \nabla_n)}$$

使用$T_t$作为训练样本集构造一棵回归树，并使用该回归树作为第$t+1$个弱学习器$L_t(X)$，该决策树中第$j$个叶子的输出值为：

$$C_{t,j}=arg_{c} min\sum_{(X_i,\nabla_i)\in T_{t}^j}J(y_i,L^t(X_i)+c)$$

其中$T_t^j$表示第$t+1$个弱学习器的第$j$个叶子节点所对应 的数据集合。

上式表明弱学习器$L_t(X)$中每个叶节点的输出均使得上轮迭代所得集成模型$L^(t-1)(X)$的预测误差达到最小

可将回归决策树$L_t(X)$表示为：

$$L_t(X)=\sum C_{t,j}[(X_i,\nabla_i)\in T_{t}^j]$$

其中：

$$I[(X_i, \nabla_i)\in T_{t}^j]=\left\{ \begin{array}{**lr**} 1, & (X_i,\nabla_i)\in T_t^j\\ 0, & (X_i,\nabla_i)\notin T_t^j \end{array} \right.$$

（4）更新集成模型为：

$$L^t(X)=L^(t-1)(X)+L_t(X)$$

若未满足算法终止条件，则返回步骤（2），否 则算法结束。

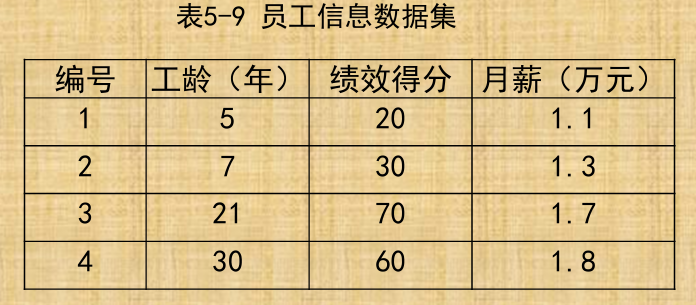
【例题】现有某个公司四位员工的考评信息即月薪如表5-9 所示，试根据该数据集和GBDT学习算法构造包含两个个体学 习器的集成模型，并使用该集成模型预测工龄为25年，绩效得 分为65分的员工的月薪。