39 核对矩阵的维数

深度学习中深度神经网络的正向传播和反向传播的过程。包含神经网络中各个层的参数和输入特性的尺寸，以及如何确保矩阵和向量的尺寸一致性。通过正向传播，我们可以计算出网络的输出和损失函数，而反向传播则用与计算梯度并更新参数。还包含深度神经网络相较于浅层表示的优势。

• 深度神经网络的调试方法，包括价差代码正确性、计算矩阵和向量的维数等。

  • 深度神经网络的搭建和维度解释

  • 矩阵运算规则和向量化实现

  • 关键概念和训练集大小

• 矩阵运算和尺寸一致性对神经网络反向传播的重要性，并提到了正向传播

  • 矩阵维度和尺寸确定：在神经网络中，确定矩阵的维度和尺寸对于实现反向传播非常重要
  • 深度神经网络的优势：深度神经网络相较于浅层表示更好，但其优势是什么？
  • 正向传播和效率：介绍了正向传播的过程，并强调了在实现深度神经网络时保持矩阵和向量尺寸的一致性可以提高效率。

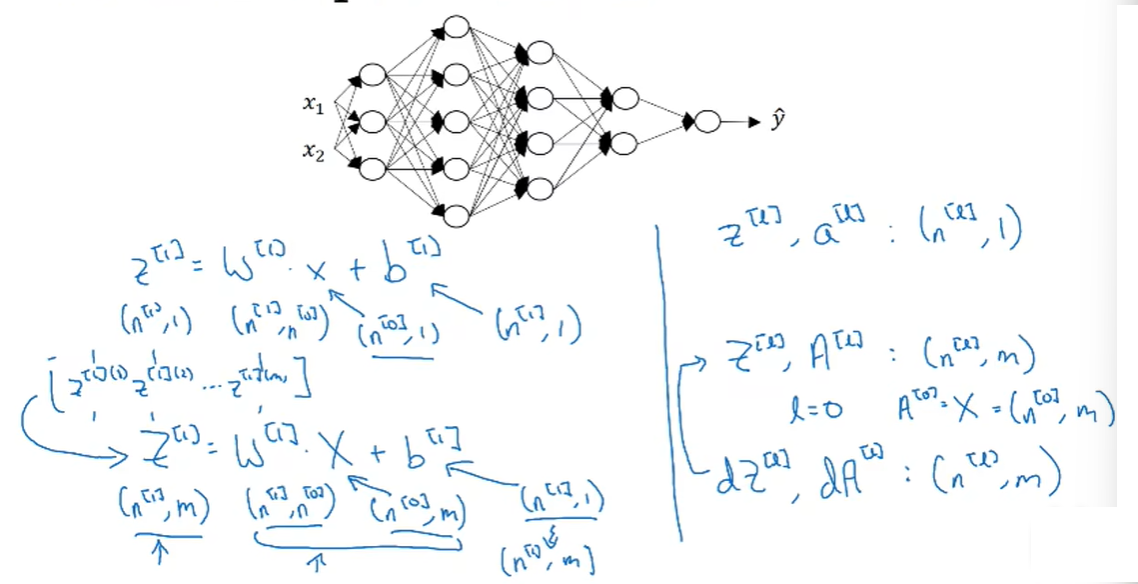
39.1 Parameters $W^{[l]} \space and \space b^{[l]}$

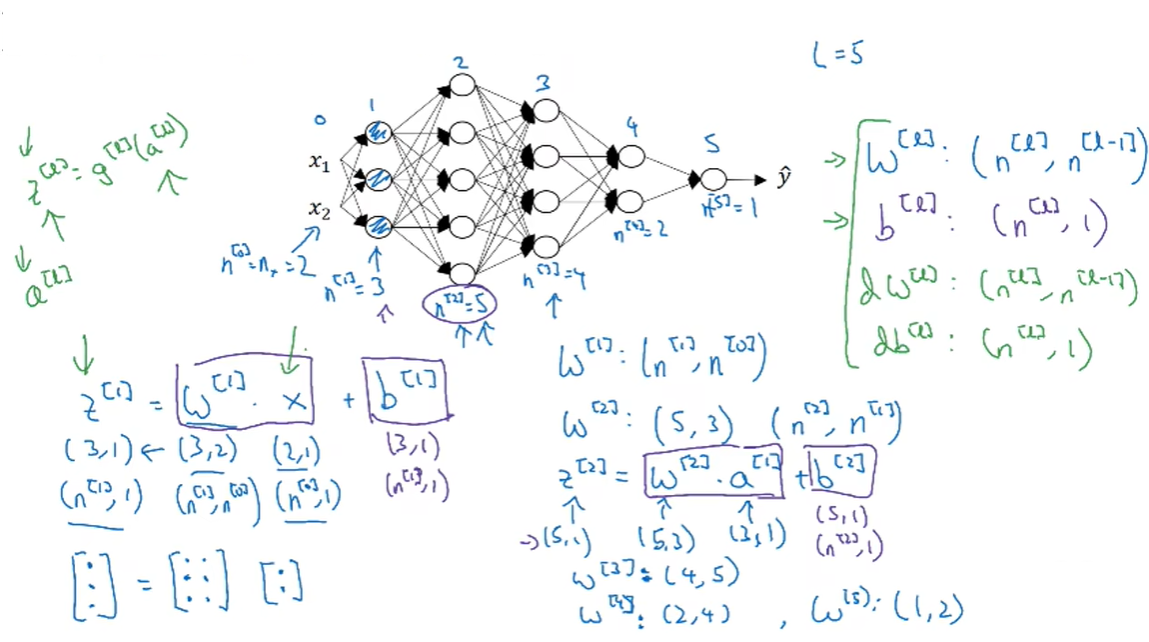
39.2 Vectorized implementation